APPLIED MATHEMATICS III

The course covers basic notions of differential equations and methods for their solution. More precisely the course covers:

i. Basic notions of ODEs. 1st order ODEs: separable, linear, exact.
ii. Linear ODEs of 2nd order, with constant coefficients, homogeneous and nonhomogeneous.
iii. Boundary value problems and eigenvalue problems. Fourier series.
iv. Systems of ODEs. Basic notions. Solution of systems of ODEs with constant coefficients, homogeneous and nonhomogeneous, by means of eigenvalues and eigenvectors.
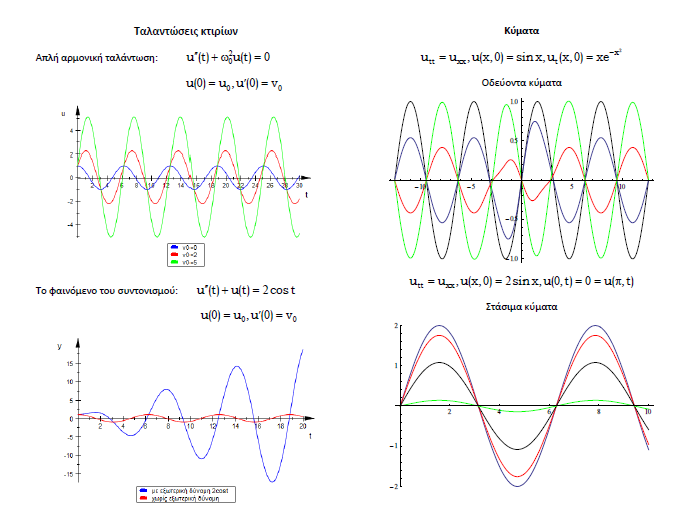
v. Basic notions and solutions of PDEs.
vi. Solution of PDEs using the separation of variables method.
vii. Laplace transform and its application to the solution of ODEs, systems of ODEs and PDEs.
viii. Fourier transform and its application to the solution of PDEs.
ix. Solution of differential equations using a scientific package of symbolic computations.
x. Applications of ODES, systems of ODEs and PDEs to problems regarding: beams, plates, oscillations, waves, heat transfer and environmental hydraulics.

Additional information
Learning Outcomes

SEMESTER	3rd
eclass	https://eclass.upatras.gr/courses/CIV1553/
Details	https://www.civil.upatras.gr/index.php/odhgos/
Instructor	PETROPOULOU EUGENIA
LANGUAGE OF INSTRUCTION and EXAMINATIONS	Greek. However, teaching may be in English for foreign (Erasmus) students attending the course.
Credits ECTS	4
Teaching Hours	4
Erasmus+	Υes
Code	CIV_3115

It is the basic course where differential equations are introduced to the students, together with analytic methods of their solutions.
During the course, the basic ideas of differential equations are introduced, together with their applications in problems relevant to civil engineering. Basic methodologies are demonstrated for finding explicit analytical solutions of both ordinary and partial differential equations. Moreover, an introduction to the Laplace and Fourier transforms is carried out with an emphasis to their use for solving specific classes of differential equations.
By the end of this course the student will be able to:
• Recognize basic problems in civil engineering which can be modelled by differential equations.
• Find explicitly analytical solutions of ordinary and partial differential equations.
• Use the Laplace and Fourier transforms.
By the end of this course the student will have developed the following skills (general abilities) (from the list above):
• Promotion of free, creative and inductive thinking
• Searching, analysis and synthesis of facts and information, as well as using the necessary technologies