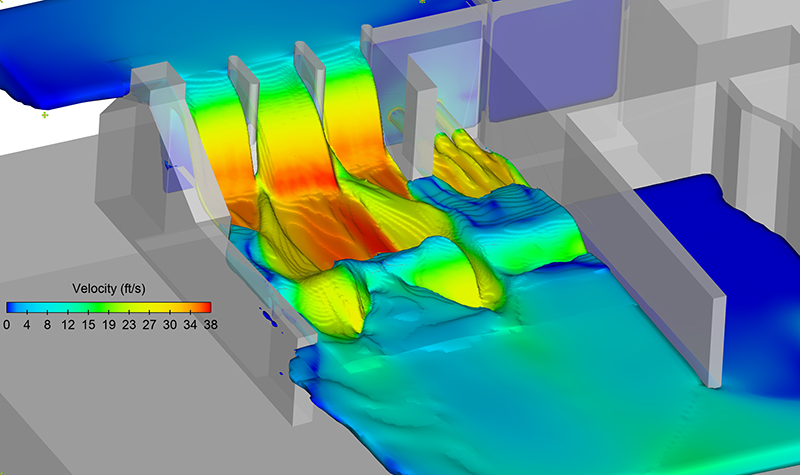
Το μαθηματικό μοντέλο στην Υδραυλική Μηχανική. Αριθμητική επίλυση αλγεβρικών εξισώσεων (κανονικό και κρίσιμο βάθος). Επέκταση σε ροή εντός δικτύων. Κανονικές διαφορικές εξισώσεις για την ανάλυση προβλημάτων σε βαθμιαίως μεταβαλλόμενη ροή, υδρολογική διόδευση ύδατος και μεταφορά μάζας σε συστήματα με πλήρη μίξη. Αριθμητική επίλυση μερικών διαφορικών εξισώσεων σε προβλήματα διάχυσης – διασποράς, ροής σε πορώδες μέσο, μη μόνιμης ροής και διαδόσεως πλημμυρικών κυμάτων, καθώς και σε προβλήματα ροής οριακού στρώματος.
ΥΠΟΛΟΓΙΣΤΙΚΗ ΥΔΡΑΥΛΙΚΗ
| Εξάμηνο Σπουδών | 8o ή 10ο |
|---|---|
| eclass | https://eclass.upatras.gr/courses/CIV1513/ |
| Λεπτομερείς Πληροφορίες | https://www.civil.upatras.gr/index.php/odhgos/ |
| Διδάσκων | ΧΟΡΣ ΓΕΩΡΓΙΟΣ |
| Γλώσσα διδασκαλίας | Ελληνική |
| Πιστωτικές μονάδες ECTS | 5 |
| Ώρες διδασκαλίας | 3 |
| Erasmus+ | ΝΑΙ |
| Κωδικός | CIV_8460A |
Στο τέλος αυτού του μαθήματος ο φοιτητής θα μπορεί να επιλύει προβλήματα της Υδραυλικής Μηχανικής με υπολογιστικές (αριθμητικές) μεθόδους όπου:
- Προκύπτουν αλγεβρικές εξισώσεις μη επιδεχόμενες αναλυτικής λύσεως (π.χ. ομοιόμορφο και κρίσιμο βάθος σε ανοικτούς αγωγούς).
- Προκύπτουν συνήθεις διαφορικές εξισώσεις (π.χ. βαθμιαίως μεταβαλλόμενη ροή σε ανοικτούς αγωγούς, υδρολογική διόδευση ύδατος μέσω ταμιευτήρα, μεταφορά ρύπων σε υδάτινα σώματα με πλήρη μίξη).
- Προκύπτουν μερικές διαφορικές εξισώσεις (π.χ. μεταγωγή και διάχυση – διασπορά ρύπων, ροή σε πορώδες μέσο, μη μόνιμη ροή σε ανοικτούς και κλειστούς αγωγούς).
- Προκύπτει η ανάγκη για χρήση ειδικών αριθμητικών τεχνικών (π.χ. ανάλυση χρονοσειράς υδραυλικών ή υδρολογικών δεδομένων, κ.λ.π.)